Рациональный банкролл-менеджмент. Часть 1.2

Перевод данной статьи был осуществлен при поддержке покер рума William Hill Poker. William Hill Покер регулярно проводит эксклюзивные турниры для своих игроков, обеспечивает поддержку пользователей 24/7, гарантирует сохранность ваших средств, а также быстрые и удобные кешауты.

2. Две составляющих банкролл-менеджмента: винрейт и дисперсия

Для создания рациональной системы банкролл-менеджмента нам потребуется предварительно ввести несколько определений. В первую очередь рассмотрим понятия винрейта (также называемого «математическим ожиданием», "EV" или просто "ожиданием") и дисперсии.

Винрейт

В покере винрейтом называется математическое ожидание выигрыша, выраженное в виде отношения выигрыша за одну игру, за 100 игр или в каких-либо других единицах. При этом мы должны различать математическое ожидание винрейта (гипотетическая величина, соответствующая случаю бесконечно долгой игры) и фактический винрейт в конкретных играх.

Винрейт зависит от того, насколько хорошо играем мы, и как играют наши оппоненты. Можно сказать, что он определяется разницей между нашим уровнем игры и усредненным уровнем игры оппонентов. Хорошие игроки в покер, в первую очередь, ищут слабых оппонентов, а потом обыгрывают их. Это искусство выбора столов и места за столами (тейбл селект) существенным образом определяет ваш винрейт.

Дисперсия

Дисперсия представляет собой статистический параметр, показывающий насколько далеко наши фактические результаты отклоняются от ожидаемых результатов. Например, пусть наше математическое ожидание винрейта в покере составляет 10 bb/100 (10 больших блайндов на 100 сыгранных игр/раздач). Означает ли это то, что после 10 000 игр наш выигрыш будет определяться выражением 10 000 x 10 bb/100 и составит ровно 1000 bb?

Нет, поскольку покер представляет собой игру со случайной составляющей (картами). В долгосрочной перспективе наши фактические (наблюдаемые) результаты будут сходиться к ожидаемым, но в краткосрочной перспективе (скажем, за несколько десятков тысяч рук или за несколько недель) очень вероятно, что фактические результаты будут существенно отличаться от ожидаемых.

Дисперсия частично представляет собой функцию случайной компоненты в игре (случайные руки), частично является функцией правил конкретной игры (некоторые покерные игры имеют более высокую дисперсию по сравнению с остальными) и частично представляет собой функцию нашего стиля игры и стилей игры оппонентов.

Если вы играете тайтово и пассивно, ваша дисперсия будет небольшой, в то время как лузово-агрессивная игра ведет к увеличению дисперсии.

Поскольку дисперсия ведет к свингам и эмоциональным стрессам, обычно принято среди игр с одинаковым ожиданием винрейта выбирать игру с меньшей дисперсией при условии, что у нас есть право выбора. Однако это не означает, что нам следует уменьшать дисперсию везде, где это возможно. Если увеличение дисперсии приводит к росту винрейта, нам следует принять более дисперсионный подход, при этом мы должны должным образом подстроить схему банкролл-менеджмента.

Хороший лузово-агрессивный игрок играет в этом стиле по причине того, что он дает ему наибольший винрейт. Естественно, он играет с большей дисперсией, чем тайтовый игрок. Большая дисперсия ведет к большим стрикам (даунстрикам и апстрикам). В итоге ему, вероятно, потребуется банкролл большего размера. Это является платой за то, что он хочет выиграть по максимуму. И он защищает свой банкролл схемой БРМ, подстроенной под его стиль игры.

У тайтового игрока дисперсия мала, что снижает даунсвинги. Означает ли это, что он может иметь меньший банкролл? Возможно, но не обязательно. Все зависит от того, приводит ли его тайтовая игра к существенному снижению винрейта.

Последнее утверждение будет нами далее рассмотрено с математической точки зрения. А сейчас давайте сформулируем два важных принципа.

• Увеличение дисперсии повышает требования к нашему банкроллу.
• Уменьшение винрейта повышает требования к нашему банкроллу.

Итак, мы хотим максимизировать наш винрейт и минимизировать нашу дисперсию. Поскольку оба требования в покере являются противоречивыми, возникает необходимость компромисса. Очевидный выбор серьезного игрока сводится к максимизации винрейта при повышенной дисперсии и использовании схемы БРМ с адекватной защитой.

Существует математическая формула (расчета риска потери банкролла), свяывающая воедино винрейт, дисперсию и требования банкролл-менеджмента. Прежде чем познакомиться с этой формулой, для улучшения нашего понимания винрейта и дисперсии рассмотрим несколько простых игр.

Начнем со строгого определения понятия винрейта.

2.1 Определение винрейта / математического ожидания

Предположим, что мы играем в игру с N различных результатами (исходами). Например, мы можем подбросить монетку, что дает два возможных исхода (орел или решка). Кроме того, предполагается, что каждый результат связан с некоторой вероятностью, выражаемой в виде числа от 0 (никогда не случается) до 1 (всегда случается). Например, при бросании монетки вероятности выпадения орла и решки равны и составляют 1/2 (50%). Пусть каждому результату игры ставится в соответствие некоторое число. Например, при выпадении орла мы выигрываем $1, при выпадении решки мы проигрываем $1.

Общее определение ожидаемого значения (математического ожидания) выигрыша для наших целей совпадает с винрейтом и может быть представлено в виде

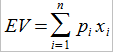
где pi - вероятности возможных N исходов, xi – значения исходов.

Другими словами, ожидаемое значение представляет собой сумму по всем возможным исходам произведений вероятности и значений каждого исхода. Для понимания формулы вычислим математическое ожидание выигрыша для следующей простейшей игры.

Математическое ожидание для Игры 1 с кубиком

• Ставка равна $1
• При выпадении 1, 2, 3 и 4 ставка возвращается (нет выигрыша и нет проигрыша)
• При выпадении 5 мы проигрываем одну ставку
• При выпадении 6 мы выигрываем две ставки

У этой игры шесть возможных исходов (на кубике может выпасть 1, 2 , 3, 4, 5, 6). Вероятности каждого из шести исходов одинаковы и составляют 1/6. Значения выигрышей для каждого исхода составляют $0 для 1, 2, 3 и 4, -$1 для 5 и +$2 для 6. Подставляем в выражение для расчета математического ожидания и получаем следующий результат.

EV (Игра 1 с кубиком) =(1/6)(0) + (1/6)(0) + (1/6)(0) + (1/6)(0) + (1/6)(-1) + (1/6)(2) =(1/6)(1) =0.1667

В этой игре мы будем выигрывать, и поэтому нам следует играть в нее. Математическое ожидание выигрыша составляет 1/6 часть от ставки, что эквивалентно $1/6 =$0.1667 за 1 бросок.

Важное свойство математического ожидания заключается в его аддитивности.

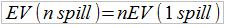
Здесь spill – испытание. В данном случае - бросок кубика. Другими словами, если мы бросаем кубик несколько раз, суммарное математическое ожидание равно сумме математических ожиданий отдельных бросков. Если в эту игру мы 100 раз бросим кубик, ожидаемое значение выигрыша составит $ 16,67:

EV (Игра 1 с кубиком, 100 бросков) = 100 (Игра 1 с кубиком, 1 бросок) = 100 (0.1667) = 16,67

Теперь, когда мы знаем для этой игры математическое ожидание выигрыша для игры, можем вычислить и дисперсию.

2.2 Определение дисперсии

Винрейт/математическое ожидание показывает наш средний ожидаемый выигрыш или проигрыш в игре. Дисперсия же показывает насколько далеко наш фактический результат может быть от ожидаемого. Для нас, игроков в покер, наибольший интерес к анализу этих величин заключается в определении величины свингов (апсвингов и, в первую очередь даунсвингов - прим. перев.) нашего банкролла.

Пусть винрейт/математическое ожидание определяется как в выше рассмотренном примере для игры с N различными исходами, для каждого из которых заданы вероятность p и значение выигрыша x. Определим дисперсию игры V в виде выражения

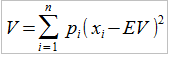
Как видно из формулы, для каждого исхода мы находим разность между его фактическим значением и математическим ожиданием, возводим ее в квадрат и умножаем на вероятность данного исхода. После этого суммируем данную величину по всем возможным исходам игры. Для Игры с кубиком 1 получаем следующий расчет дисперсии игры:

V (Игра с кубиком 1) 

= (1/6) (0 - 0,1677) ^ 2 + (1/6) (0 - 0,1677) ^ 2 

+ (1/6) (0 - 0,1677) ^ 2 + (1/6) (0 - 0,1677) ^ 2 

+ (1/6) (- 1 - 0,1677) ^ 2 + (1/6) (2 - 0,1677) = 2

 = 0,8056

Как и математическое ожидание, дисперсия обладает свойством аддитивности. Полная дисперсия после серии бросков кубика находится путем суммирования дисперсий отдельных бросков:

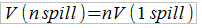
Таким образом, дисперсия для 100 бросков в игре с кубиком 1 может быть представлена в виде произведения 100 и дисперсии при одном броске:

V (Игра с кубиком 1, 100 бросков)

= 100 (0.8056)

= 80.56

Теперь нам осталось дать определение еще одной величины – среднеквадратическому отклонению SD (standard deviation).

2.3 Определение среднеквадратического отклонения

Среднеквадратическим отклонением называется квадратный корень из дисперсии:

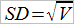
Среднеквадратическое отклонение и дисперсия по сути являются двумя путями измерения одного и того же – разности между ожидаемыми и фактическими значениями. В формулах расчета статистических величин чаще встречается среднеквадратическое отклонение, так что нам следует дать его расчет для модельного примера.

Ниже приведен расчет для среднеквадратического отклонения для игры с кубиком 1.

SD (Dice Game 1)

= Sqrt (0,8056)

= 0,8975

Здесь Sqrt представляет собой операцию квадратного корня. В отличие от математического ожидания и дисперсии, среднеквадратическое отклонение не обладает свойством аддитивности, как показано ниже:

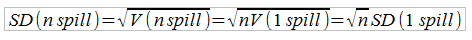
Таким образом, если мы 100 раз бросим кубик в игре 1, суммарное среднеквадратическое отклонение равно произведению среднеквадратического отклонения одного броска на sqrt(100)=10:

SD (Игра с кубиком 1, 100 бросков)

= Sqrt (100) (0,8975)

= 10 (0.8975)

= 8,975

Итак мы определили все статистические величины, которые будут использоваться во всех статьях этой серии при анализе применения схем банкролл-менеджмента для различных игр.

В следующих статьях мы рассмотрим в деталях, как математическое ожидание и среднеквадратическое отклонение будут использоваться для расчета требований к схеме управления банкролла.

Перевод: Сергей 'ivolga' специально для pokeristby