Рациональный банкролл-менеджмент. Часть 1.3

Перевод данной статьи был осуществлен при поддержке покер рума William Hill Poker. William Hill Покер регулярно проводит эксклюзивные турниры для своих игроков, обеспечивает поддержку пользователей 24/7, гарантирует сохранность ваших средств, а также быстрые и удобные кешауты.

Итак, в части 1.2 мы определили все статистические величины, которые будут использоваться во всех статьях этой серии при анализе применения схем банкролл-менеджмента для различных игр. В следующих статьях мы рассмотрим в деталях, как математическое ожидание и среднеквадратическое отклонение будут использоваться для расчета требований к схеме управления банкролла.

Но перед этим давайте проведем небольшое исследование дисперсии в разных играх с кубиком. Пусть во второй игре с кубиком винрейт останется таким же, как и в игре 1, а значение дисперсии будет иным.

3. Анализ изменения дисперсии

Определим условия новой игры. В игре с кубиком 2 мы проигрываем ставку при выпадении 1, 2, 3, 4 и 5. А при выпадении 6 выигрываем сразу 6 ставок. Математическое ожидание, дисперсия и среднеквадратическое отклонение для игры 2 вычисляются следующим образом.

EV (Игра с кубиком 2)

= (1/6) (- 1) + (1/6) (- 1) + (1/6) (- 1) + (1/6) (- 1)

+ (1/6) (- 1) + (1/6) (6)

= (1/6) (1)

= 0,1667

Математическое ожидание выигрыша для игры 2 совпадает с соответствующим значением для игры 1 и равно +$0.1667. Однако дисперсия и среднеквадратическое отклонение существенно увеличиваются по сравнению с предыдущей игрой:

V (Игра с кубиком 2)

= (1/6) (- 1 - 0,1677) ^ 2 + (1/6) (- 1 - 0,1677) = 2

+ (1/6) (- 1 - 0,1677) ^ 2 + (1/6) (- 1 - 0,1677) = 2

+ (1/6) (- 1 - 0,1677) ^ 2 + (1/6) (6 - 0,1677) = 2

= 6,8056

SD (Игра с кубиком 2)

= Sqrt (6,8056)

= 2,6087

Давайте подведем итог и сравним условия и результаты двух игр с кубиком.

Игра с кубиком 1

Ставка в игре равна $1.

• При выпадении 1, 2, 3 и 4 ставка возвращается.
• При выпадении 5 мы проигрываем ставку.
• При выпадении 6 мы выигрываем две ставки.
• Математическое ожидание выигрыша EV = 0.1667.
• Дисперсия V = 0.8056.
• Среднеквадратическое отклонение SD = 0.8975.

Игра с кубиком 2

Ставка в игре равна $1.

• При выпадении 1, 2, 3, 4 и 5 мы проигрываем ставку.
• При выпадении 6 мы выигрываем шесть ставок.
• Математическое ожидание выигрыша EV = 0.1667.
• Дисперсия V = 6.8056.
• Среднеквадратическое отклонение SD = 2.6087.

Во второй игре (игра с кубиком 2) дисперсия больше чем в 8 раз выше по сравнению с первой игрой (игра с кубиком 1). Соответственно выше и среднеквадратическое отклонение. Как могут для нас различаться результаты каждой из этих игр?

Ответ на этот вопрос следует из самого принципа рационального банкролл-менеджмента. Большинство читателей интуитивно поймут, что при наличии свободы выбора в какую игру играть, следует выбрать первую игру. Для второй игры возможны даунсвинги большего размера без каких-либо дополнительных преимуществ. Большие даунсвинги при ограниченном финансировании игры могут привести к большим проблемам.

Предположим, что мы выделили на игру сумму в $5. В первой игре с кубиком к проигрышу ведет один единственный исход. В 5 случаях из 6 мы либо ничего не выигрываем, либо ничего не проигрываем (возврат ставки), либо выигрываем двойную ставку. Риск потери банкролла до того, как мы сможем значительно его увеличить, чтобы пережить даунсвинги, достаточно мал.

Однако во второй игре мы проигрываем ставку в 5 случаях из 6. В долгосрочном плане выигрыш в обеих играх будет одинаков. Однако велика вероятность того, что долгосрочной игры может и не быть, поскольку мы просто можем быстро потерять весь банкролл на даунсвингах. Говоря иначе, обе игры одинаково прибыльны, однако в игре с большей дисперсией реализовать потенциальный выигрыш будет сложнее (если начальный банкролл небольшой).

Конечно, при значительной величине начального банкролла фактор большой дисперсии не важен. Мы по-прежнему выберем первую игру, поскольку выбирать при одинаковом ожидаемом винрейте более дисперсионную игру нет смысла. Однако, этот выбор будет продиктован общими логическими соображениями, а не необходимостью защитить свой банкролл (поскольку мы обладаем значительным начальным банкроллом).

В конце первой статьи мы приводим графические иллюстрации влияния дисперсии на результаты двух игр с кубиками. Все графики выполнены при помощи онлайнового симулятора дисперсии в покере (на день перевода ссылка неактивна – прим. перев.).

Для работы симулятора требуются значения «за 100 рук». Вычислим необходимые значения математического ожидания и среднеквадратического отклонения. Поскольку математическое ожидание аддитивно, величина математического ожидания EV за 100 бросков кубика представляется в виде 100 х EV для одного броска, что в итоге дает 100 х 0,1667 = 16,67 за 100 бросков. Для обеих игр эта величина одинакова.

С ростом числа повторений среднеквадратическое отклонение растет как квадратный корень от числа повторений, согласно приведенным выше формулам. Таким образом, среднеквадратическое отклонение при 100 бросках кубика можно представить в виде произведения коэффициента 10, получаемого как sqrt(100) и среднеквадратического отклонения для одного броска. В итоге мы получаем значения среднеквадратического отклонения SD = 10 (0.8975) = 8,975 для первой игры и 10 (2,6087) = 26,087 для второй игры

Для обеих игр будем рассматривать ситуацию, когда 10 игроков бросают кубик 1000 раз каждый, для чего параметры симулятора “Num. of trials to run” (Число испытаний) и “Num of hands” (Число рук) выберем как 10 и 1000 соответственно. Ниже представлены графики выигрышей для всех 10 игроков.

3.1 Моделирование дисперсии для игры 1

Расшифровка всех подписей для картинок находится в конце статьи

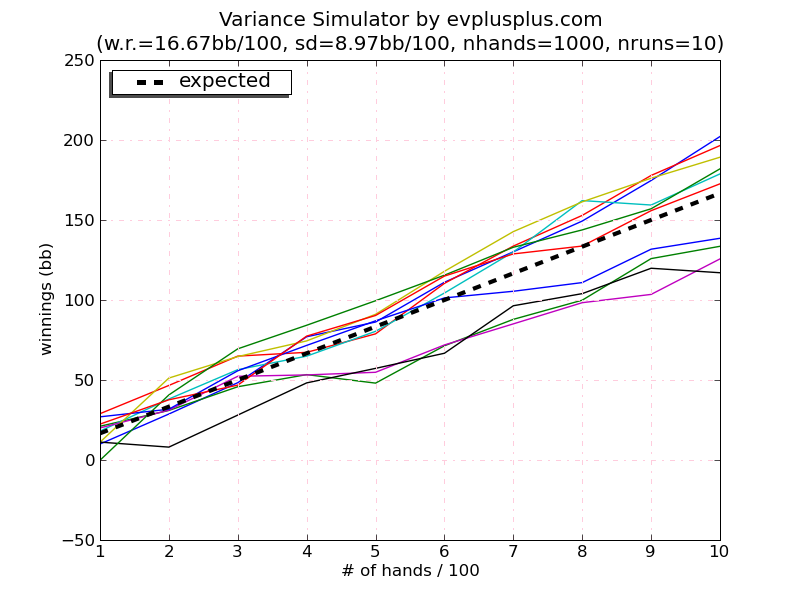
Математическое ожидание после 1000 бросков равно 1000 х 0,1667 = + $ 166,70. Зависимость математического ожидания от числа сыгранных рук на графике представлена пунктирной линией. Мы видим, что фактические результаты наших 10 игроков находятся вокруг ожидаемых значений, при этом фактические выигрыши находятся в интервале от + $ 115 до $ 200. Наибольшее отрицательное отклонение от величины ожидаемого выигрыша составило около $ 52.

Несмотря на то, что математическое ожидание выигрыша для всех игроков составляло + $ 166,70 на 1000 бросков, фактические значения выигрышей сильно разбросаны вокруг ожидаемого значения. Шесть игроков выиграли больше ожидаемого значения, и четыре игрока выиграли меньше. Это является следствием моделирования случайного распределения, при этом новое моделирование с этими же входными данными даст, конечно же, другие фактические результаты.

Если мы увеличим число бросков до 10 000, то получим следующие результаты.

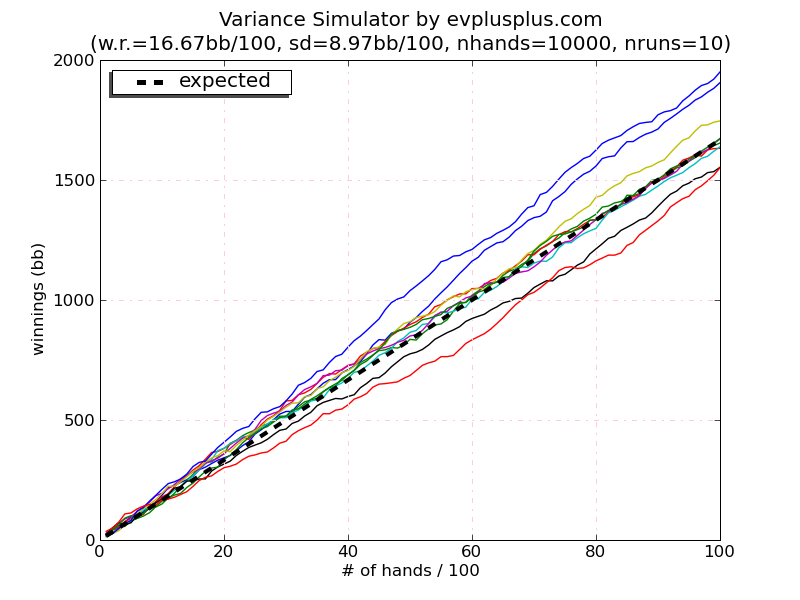
Все 10 игроков имеют существенные выигрыши. Фактические выигрыши изменяются в интервале от +$ 1550 до +$1950 при математическом ожидании выигрыша 10000 х 0,1667 = + $ 1667. При этом моделировании разброс результатов уменьшился по сравнению с результатами первого моделирования.

Наибольшее отклонение от ожидаемого выигрыша составило $238 выше ожидаемого значения, в то время как при моделировании 1000 бросков наибольшее отклонение составляло $52 ниже ожидаемого значения. При втором моделировании отклонение $283 от ожидаемого значения $ 1667 (относительное отклонение 283/1667 = 17%) в относительном значении оказалось меньше отклонения $52 от ожидаемого значения $166.70 (относительное отклонение 52 / 166,7 = 31%) по сравнению с первым моделированием. Это подтверждает то, что относительное отклонение от ожидаемого значения уменьшается с ростом числа бросков.

Последнее наблюдение является следствием большого числа испытаний. Чем больше мы играем, тем ближе наши фактические результаты приближаются к ожидаемым значениям. С математической точки зрения, это является следствием того, что наш выигрыш от числа бросков растет линейно (свойсво аддитивности математического ожидания), в то время как среднеквадратическое отклонение не обладает свойством аддитивности и растет более медленно, как квадратный корень от числа бросков, как это было показано выше в формуле.

После мы провели аналогичные моделирования для игры с кубиком 2 с тем же математическим ожиданием выигрыша, но с увеличенными значениями дисперсии и среднеквадратического отклонения.

3.2 Моделирование дисперсии для игры 2

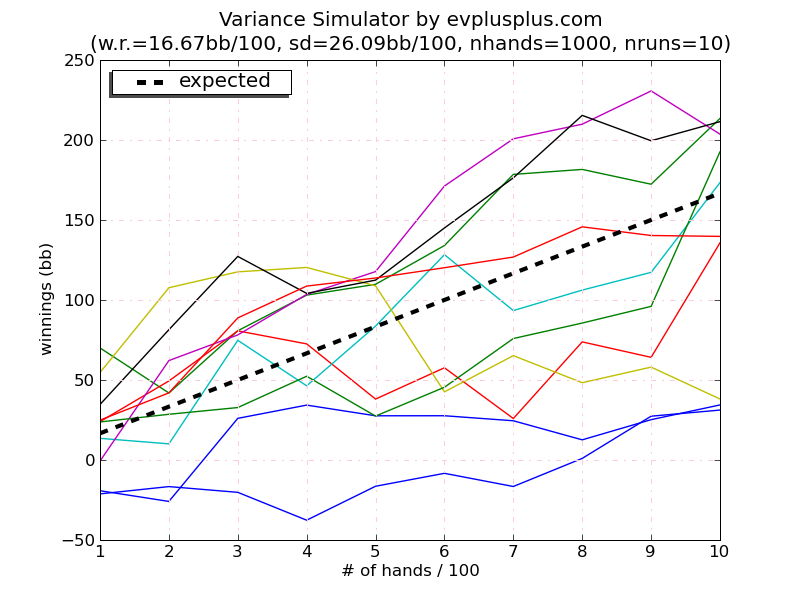
Ниже представлены результаты моделирования для 1000 бросков.

Разброс величин выигрышей 10 игроков после 1000 испытаний по сравнению с первой игрой существенно увеличился с $35 до $210. Наибольшее отклонение составило $132 вниз от ожидаемого значения $166.70. На графике наглядно видно, что значения выигрышей игроков стали более хаотичными по сравнению с соответствующим моделированием первой задачи.

После этого мы увеличили число рук до 10 000 и получили следующие результаты.

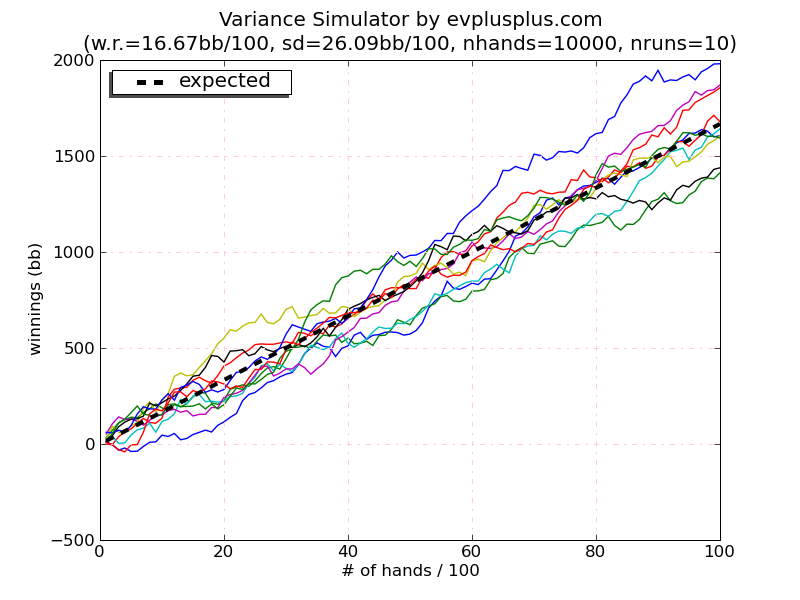
Разброс выигрышей составляет от + $ 1400 до + 2000 $, при этом наибольшее отклонение составляет около $ 333 вверх от ожидаемого результата. Для Игры в кубики 1 показатели разброса составляли $1550 и $1950 соответственно, при этом максимальное отклонение составляло $283 вверх от ожидаемого значения. При увеличении числа бросков до 10 000 увеличенная дисперсия во второй игре также приводит к большому разбросу результатов.

3.3 Выводы по моделированию дисперсии для игр с кубиком

Произведенное нами моделирование с точно известными значениями математического ожидания и среднеквадратического отклонения для двух игр с кубиком должны были вызвать интерес к следующим статьям этой серии. Мы увидели, что игры с одинаковым винрейтом могут иметь много различных графиков выигрыша, и эти отличия, в первую очередь, обусловлены различием значений дисперсии.

В следующих статьях мы займемся исследованиями винрейта/математического ожидания и дисперсии/среднеквадратического отклонения в покере. В реальных играх эти величины вычисляются значительно более сложным способом, чем в двух наших упрощенных играх, и на практике для них нельзя получить точные значения. Однако мы всегда можем получить их оценки из трекерных программ (таких как HoldemManager или PokerTracker). И эти оценки мы можем использовать для анализа схем БРМ.

Следующая наша задача будет заключаться в изучении способов использования в требованиях БРМ в покере таких показателей как винрейт и среднеквадратическое отклонение. В Части 3 мы рассмотрим формулу оценки риска потери банкролла. Однако до этого мы в Части 2 займемся исследованиями того, как наши определения математического ожидания, дисперсии и среднеквадратического отклонения работают в простейших покерных играх типа AKQ-игр.

4. Заключение

Мы начали наше обсуждение принципов рационального ведения банкролла. В этой статье мы определили проблему банкролл-менеджмента и получили на примере двух простейших игр с кубиком общее представление о винрейте/математическом ожидании и дисперсии/ среднеквадратическом отклонении. Было показано, как для этих игр получить точные значения указанных выше параметров.

Во второй части мы обсудим, каким образом наши определения винрейта, дисперсии и среднеквадратического отклонения можно будет определить в покерных играх. Все расчеты будут проводиться на примере простейшей покерной AKQ-игры с одним раундом лимитированных ставок.

Удачи всем!

Багз

Примечания к изображениям (Общие надписи на всех рисунках)

Изображения были получены при помощи симулятора дисперсии от evplusplus.com, однако на момент перевода статьи данный сайт был закрыт. Если выжелаете провести похожие исследования, советуем вам воспользоваться аналогичным симулятором от PokerDope.

w.r. – винрейт

sd – среднеквадратическое отклонение

nhands – число рук

nruns – число игроков

expected – математическое ожидание выигрыша

winnings (bb) – выигрыш (bb)

# of hands / 100 – число рук / 100

Перевод: Сергей 'ivolga' специально для pokeristby