Рациональный банкролл-менеджмент. Часть 2.1

Перевод данной статьи был осуществлен при поддержке покер рума William Hill Poker. William Hill Покер регулярно проводит эксклюзивные турниры для своих игроков, обеспечивает поддержку пользователей 24/7, гарантирует сохранность ваших средств, а также быстрые и удобные кешауты.

1. Введение

Данная статья является второй в серии статей о банкролл-менеджмент (БРМ) в покере. В первой части мы дали определения математического ожидания, дисперсии и среднеквадратического отклонения. Для игры с n возможными исходами, каждому из которых ставится в соответствие вероятность p и значение x, можно записать следующие выражения для расчета математического ожидания, дисперсии и среднеквадратического отклонения.

Математическое ожидание

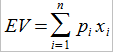
Дисперсия

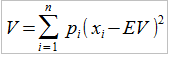
Среднеквадратическое отклонение

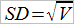
Для исследования этих формул в Части 1 мы задали условия двух простых игр с кубиком, для которых математические ожидания выигрыша совпадали, а дисперсии различались. После чего рассчитали значения математического ожидания, дисперсии и среднеквадратического отклонения для обеих игр.

Игра с кубиком 1

Ставка в игре равна $1.

• При выпадении 1, 2, 3 и 4 ставка возвращается.
• При выпадении 5 мы проигрываем ставку.
• При выпадении 6 мы выигрываем две ставки.
• Математическое ожидание выигрыша EV = 0.1667.
• Дисперсия V = 0.8056.
• Среднеквадратическое отклонение SD = 0.8975.

Игра с кубиком 2

Ставка в игре равна $1.

• При выпадении 1, 2, 3, 4 и 5 мы проигрываем ставку.
• При выпадении 6 мы выигрываем шесть ставок.
• Математическое ожидание выигрыша EV = 0.1667.
• Дисперсия V = 6.8056.
• Среднеквадратическое отклонение SD = 2.6087.

Мы сделали это, чтобы показать каким образом определения математического ожидания, дисперсии и среднеквадратического отклонения можно использовать для анализа простых игр. Можно сказать, что мы научились вычислять эти значения в зависимости от условий и правил игры.

2. Математическое ожидание, дисперсия и среднеквадратическое отклонение в покере

Для реальных покерных игр провести расчет математического ожидания, дисперсии и среднеквадратического отклонения на основании одних лишь базовых формул практически невозможно, поскольку нам пришлось бы составить список всех возможных исходов, и каждому из них поставить в соответствие значения вероятностей и выигрыша.

Для реальных покерных игр расчет вероятности и выигрыша одного отдельного исхода уже представляется чрезвычайно сложной задачей. Но если бы мы с ней и справились, астрономическое количество возможных исходов в игре сделает расчет невыполнимым. Для примера, в хедз-ап (heads-up – игра один на один, прим. перев.) играх в лимитном Холдеме возможно около 10 ^ 18 исходов. А это одна из простейших покерных игр для теоретического анализа!

Описание полных стратегий игры для всех игроков, вычисление вероятностей и выигрышей для миллиардов исходов на практике представляется невозможным. Для упрощения задачи мы возьмем значения математического ожидания, дисперсии и среднеквадратического отклонения из программ PokerTracker или HoldemManager. В этих программах статистические оценки рассчитаны на основе анализа наших сыгранных рук, и мы можем считать их лучшими оценками.

Прежде чем перейти к анализу покерных игр, рассмотрим модель простейшей игры в покер. На ее основе покажем, как следует использовать определения математического ожидания, дисперсии и среднеквадратического отклонения в покерных играх.

3. Математическое ожидание, дисперсия и среднеквадратическое отклонение для AKQ-игры с фиксированными ставками для двух улиц

Займемся расчетом математического ожидания, дисперсии и среднеквадратического отклонения для AKQ-игры с фиксированными ставками для двух улиц. Это простая игра, которую мы тщательно исследовали в серии статей «Modeling Poker» (Моделирование покерных игр).

3.1 Условия игры

• В игру играют два игрока: Алиса (вне позиции) и Боб (в позиции).
• В начале игры оба игрока ставят анте в n bb. Это формирует начальный пот P = 2n bb.
• Оба игрока получают по одной случайной карты из AKQ-колоды.
• Алиса чекает "втемную".
• Теперь Боб может чекнуть и посмотреть шоудаун, а может и поставить 1 bb.
• Если Боб ставит 1 bb, Алиса может сфолдить, а может заколлировать ставку Боба и посмотреть шоудаун.
• После окончания раунда ставок, если никто из игроков не сфолдил, на шоудауне побеждает старшая карта.

Ниже приведен расчет статистических параметров в предположении, что оба игрока играют оптимальным образом.

3.2 Анализ AKQ-игры с фиксированными ставками для двух улиц

Алиса

• С тузом всегда играет Чек/Колл.
• С королем играет Чек/Колл в случаях (Р - 1) / (Р + 1), где P-размер пота.
• С дамой всегда играет Чек/Фолд.

Боб

• С тузом всегда ставит на велью.
• С королем чекает в ответ на чек Алисы.
• С дамой блефует в случаях 1 / (Р + 1 ), где P-размер пота.

Математическое ожидание выигрыша Боба:

ЕV= (1/6) (Р-1) / (Р + 1)

В этой статье мы рассмотрим только игру с  анте в 1 bb. Таким образом, до начала ставок пот P составляет 2 bb.

3.3 Расчет математического ожидания, дисперсии и среднеквадратического отклонения для AKQ-игры

Для анализа AKQ-игры выберем схему исследования  двух игр с кубиком в Части 1. Сначала мы рассмотрим все возможные исходы, найдем соответствующие вероятности и значения выигрышей. После чего подставим эти значения в формулы для расчета математического ожидания, дисперсии и среднеквадратического отклонения. Значения всех параметров будем рассчитывать для Боба.

После окончания этого этапа расчетов мы получим точные значения искомых статистических величин для простой покерной игры. Это послужит иллюстрацией применения математического ожидания, дисперсии и среднеквадратического отклонения в покере. В реальном покере все обстоит значительно сложнее, однако основополагающие принципы не меняются.

Мы видим, что в игре возможно 6 различных сценариев:

• Сценарий 1: У Алисы туз, у Боба король.
• Сценарий 2: У Алисы туз, у Боба дама.
• Сценарий 3: У Алисы король, у Боба туз.
• Сценарий 4: У Алисы король, у Боба дама.
• Сценарий 5: У Алисы дама, у Боба туз.
• Сценарий 6: У Алисы дама, у Боба король.

Все сценарии равновероятны, поэтому вероятность каждого из них составляет 1/6. Остается вычислить значения выигрыша Боба для каждого сценария. Выше описано, как играют Алиса и Боб в каждом из возможных сценариев игры.

Для каждого сценария запишем выражения для математического ожидания и вычислим выигрыш или проигрыш Боба для каждого из них. Заметим, что мы приводим расчет математического ожидания для всей игры, а не только для раунда ставок.

Сценарий 1: у Алисы туз, у Боба король

EV1 = (1/6) {- 1}

Боб всегда чекает в ответ на чек Алисы, в результате чего он проигрывает анте. Результат игры: -1 bb.

Сценарий 2: у Алисы туз, у Боба дама

EV2
= (1/6) {(2/3) (- 1) + (1/3) (- 2)}
= (1/6) {- 4/3}

Боб с дамой чекает в 2/3 случаев и проигрывает 1 bb анте. В 1/3 случаев он блефует и кроме анте проигрывает ставку. Результат игры при этом составляет -2 bb.

Сценарий 3: у Алисы король, у Боба туз

EV3
= (1/6) {(1/3) (+ 2) + (2/3) (+ 1)}
= (1/6) {4/3}

Боб всегда ставит. Алиса коллирует его ставку в  1/3 случаев, после чего Боб выигрывает анте Алисы и ее ставку. Результат игры: +2 bb. В оставшихся 2/3 случаев Алиса фолдит, и Боб выигрывает ее анте, при этом результат игры: +1 bb.

Сценарий 4: у Алисы король, у Боба дама

EV4
= (1/6) {(2/3) (- 1) + (1/3) {(1/3) (- 2) + (2/3) (+ 1)}}
(1/6) {- 2/3 + (1/3) {0}}
= (1/6) {- 2/3}

В 2/3 случаев Боб чекает в ответ на чек Алисы и теряет анте. Результат игры: -1 bb. В 1/3 случаев он блефует. В 1/3 случаев Алиса коллирует, и Боб проигрывает анте и ставку. Результат игры:  – 2 bb. В оставшихся 2/3 случаев Алиса фолдит, и Боб выигрывает ее анте. Результат игры: +1 bb.

Сценарий 5: у Алисы дама, у Боба туз

EV5 = (1/6) {+ 1}

Боб всегда ставит, Алиса всегда фолдит. Боб выигрывает анте Алисы. Результат игры: +1 bb.

Сценарий 6: у Алисы дама, у Боба король

EV6 = (1/6) {+ 1}

Боб всегда чекает в ответ с королем и выигрывает анте Алисы. Результат игры: +1 bb.

В итоге мы получаем следующий список возможных исходов для AKQ-игры:

• Сценарий 1:  у Алисы туз, у Боба король.
      - Вероятность: 1/6.
      - Результат Боба: -1 ​​bb.

• Сценарий 2: у Алисы туз, у Боба дама.
      - Вероятность: 1/6.
      - Результат Боба: -4/3 bb.

• Сценарий 3: у Алисы король, у Боба туз.
      - Вероятность: 1/6.
      - Результат Боба: +4/3 bb.

• Сценарий 4: у Алисы король, у Боба дама.
      - Вероятность: 1/6.
      - Результат Боба: -2/3 bb.

• Сценарий 5: у Алисы дама, у Боба туз.
      - Вероятность: 1/6.
      - Результат Боба: +1 bb.

• Сценарий 6: у Алисы дама, у Боба король.
      - Вероятность: 1/6.
      - Результат Боба: +1 bb.

Подставим эти значения в формулы для вычисления математического ожидания, дисперсии и среднеквадратического отклонения:

Расчет математического ожидания

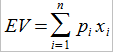
EV

= (1/6) {- 1} + (1/6) {- 4/3} + (1/6) {4/3}
+ (1/6) {- 2/3} + (1/6) {+ 1} + (1/6) {+ 1}
= (1/6) {- 1 -4/3 +4/3 -2/3 + 1 + 1}
= (1/6) {1/3}
= 1/18

В покере винрейт принято смотреть на 100 сыгранных рук. В соответствии с этим правилом математическое ожидание выигрыша составляет EV = 100/18 bb / 100 = 5,56 bb / 100.

Подставим значение математического ожидания в формулу для расчета дисперсии.

Расчет дисперсии

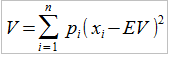
V
= (1/6) {- 1 - 1/18} ^ 2 + (1/6) {- 4/3 - 1/18} ^ 2
+ (1/6) {4/3 - 1/18} ^ 2 + (1/6) {- 2/3 - 1/18} ^ 2
+ (1/6) {1 - 1/18} ^ 2 + (1/6) {1 - 1/18} ^ 2
= 1,1636

Дисперсия нам нужна исключительно для расчета среднеквадратического отклонения, поскольку в статистическом анализ покерных игр обычно используется среднеквадратическое отклонение.

Расчет среднеквадратического отклонения

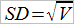
SD = sqrt (1,1636) = 1,0787, где sqrt – операция квадратного корня.

Выразим в следующей формуле среднеквадратическое отклонение в единицах «bb/100»

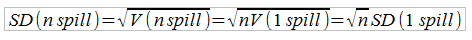
Здесь n spill – число испытаний.

SD (100 рук) = sqrt (100) SD (1 рука) = 10 (1,0787) = 10,787

Перевод: Сергей 'ivolga' специально для pokeristby