Рациональный банкролл-менеджмент. Часть 3.1

Перевод данной статьи был осуществлен при поддержке покер рума William Hill Poker. William Hill Покер регулярно проводит эксклюзивные турниры для своих игроков, обеспечивает поддержку пользователей 24/7, гарантирует сохранность ваших средств, а также быстрые и удобные кешауты.

1. Введение

Данная статья является второй в серии статей о банкролл-менеджмент (БРМ) в покере. В первой части мы дали определения математического ожидания, дисперсии и среднеквадратического отклонения. Для игры с n возможными исходами, каждому из которых ставится в соответствие вероятность p и значение x, можно записать следующие выражения для расчета математического ожидания, дисперсии и среднеквадратического отклонения.

Математическое ожидание

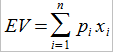
Дисперсия

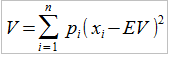
Среднеквадратическое отклонение

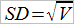
Цель данной работы заключалась в исследовании статистических свойств математического ожидания и дисперсии/среднеквадратического отклонения (двух величин, характеризующих одно и то же свойство). Мы узнали, как их можно рассчитать для любой игры. Кроме того, увидели на графиках, как рост дисперсии приводит к увеличению колебаний банкролла.

На примере двух игр с кубиком было показано, как две игры могут иметь одно и то же значение математического ожидания и разные дисперсии. Графический анализ результатов работы онлайн симулятора дисперсии показал, что ожидаемый выигрыш в двух играх одинаков, но распределения разброса значений различны. В игре с большой дисперсией разброс значений выигрыша вокруг ожидаемого значения оказался значительно бОльшим по сравнению со случаем малой дисперсии.

В Части 3 мы познакомимся с новым понятием – «риском разорения» (РР) и рассмотрим математическую формулу, в которой связаны воедино значения математического ожидания, среднеквадратического отклонения, риск разорения и величина банкролла. Необходимый для игры банкролл является функцией математического ожидания, среднеквадратического отклонения и нашей толерантности к риску. Если эти значения известны, мы можем рассчитать значение необходимого банкролла.

Предварительно познакомимся с формулой для расчета риска разорения.

2. Формула для риска разорения

Приведем без вывода формулу для расчета риска разорения

Где

R = риск разорения.
B = величина банкролла.
W = винрейт.
S = среднеквадратическое отклонение.

Обозначение "R (B)" означает, что R является функцией от В. Часто говорят “R при данном В” или “R при известном В”.

Итак, мы играем в игру, где W - наш фактический винрейт (считаем его синонимом математического ожидания), S – среднеквадратическое отклонение, В – величина банкролла. Данная формула позволяет рассчитать вероятность R(B) потери банкролла В в будущем.

Важный нюанс (не будем вдаваться в подробности) состоит в том, что при выводе формулы РР предполагалось, что результаты игры подчиняются нормальному распределению. Распределение выигрышей в покер не является нормальным, но для оценки требований к величине банкролла будем считать, что формула РР достаточно хорошо применима к реальным покерным играм.

В формуле для расчета риска разорения подразумевается, что величины W и S являются константами. Таким образом, риск разорения фактически является функцией от одного аргумента – величины банкролла В. Это соответствует нашему представлению о винрейте и среднеквадратическом отклонении в покере. Мы предполагаем, что обе величины являются константами для конкретной игры, в которую мы играем. При этом их точные значения для нас неизвестны. Оценки этих величин можем получить из программ PokerTracker или HoldemManager. Но для получения точных оценок (в частности, для винрейта) нам потребовалось бы сыграть большое количество игр.

Заметим, что в формуле предполагается отсутствие кешаутов. В противном случае наш эффективный винрейт оказался бы меньше теоретического, и нам пришлось бы скорректировать формулу путем замены винрейта на эффективный винрейт.

Также важно обратить внимание на следующий нюанс. Если мы кешаутим весь выигрыш и сохраняем текущий банкролл равным начальному, это эквивалентно тому, что в формуле РР мы можем взять нулевое значение винрейта W. В этом случае вероятность потери банкролла становится равной 100%:

Таким образом, если мы кешаутим все наши выигрыши и поддерживаем банкролл постоянным, мы гарантированно разоряемся независимо от размера стартового капитала. Это может показаться странным, однако логика здесь проста. Существует конечная ненулевая вероятность попасть в даунсвинг любого размера. При неограниченной длительности игры рано или поздно мы столкнемся с даунсвингом, который полностью «съест» наш банкролл. Если мы используем большой статический банкролл, это может произойти не скоро (может быть, даже не в этой жизни!), однако катастрофа с потерей банкролла неизбежно произойдет в будущем. 

При полном отсутствии кешаутов наш банкролл будет расти, и накопленный капитал позволит пережить большие даунсвинги. По мере роста банкролла улучшается защита от даунсвингов. В итоге, риск разорения никогда не становится равным нулю. С ростом банкролла вероятность разорения всегда остается меньше 100%.

Следует отметить, что в случае статического банкролла мы всегда можем защитить себя гарантированного разорения путем перехода на более низкий лимит, когда этот риск становится недопустимо высоким для игры на текущем лимите. Формула риска разорения не утверждает, что мы потеряем статический банкролл в обозримом будущем. Она лишь показывает, что если мы продолжаем играть на этом же лимите и кешаутим все выигрыши, потеря банкролла произойдет в принципе. Однако заметим, что у нас всегда остается капитал от кешаутов.

Мы не будем обсуждать стратегии переходов вверх и вниз по лимитам, поскольку это будет описано в другой статье данной серии. До этого будем применять формулу риска разорения, считая, что мы продолжаем играть на текущем лимите с известными значениями винрейта и среднеквадратического отклонения.

На основе этой формулы можем получить выражение для размера банкролла R, необходимого  для игры с заданным риском разорения R. Далее приведены соответствующие вычисления.

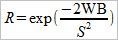
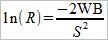
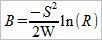
Это выражение можно представить в следующем виде

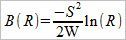
Здесь B (R) означает, что В является функцией от аргумента R. В этом выражении в числителе дроби вместо квадрата среднеквадратического отклонения, мы могли бы использовать дисперсию V, поскольку  V = S ^ 2.

Из этой формулы видим, что размер банкролла определяется не дисперсией (квадратом среднеквадратического отклонения), а отношением дисперсии к винрейту. Одновременное увеличение дисперсии и винрейта не приводит к необходимости иметь банкролл большего размера. Например, увеличение дисперсии (S ^ 2) в два раза с одновременным удвоением винрейта не приведет к изменению риска разорения (и, соответственно, ожидаемых свингов).

Дисперсия в пот-лимитной Омахе (PLO) выше, чем дисперсия в безлимитном Холдеме (NLHE). В настоящее время средний уровень игроков в PLO ниже, чем в NLHE, поскольку NLHE оставался популярнейшей покерной игрой в течение многих лет. Таким образом, не следует бояться увеличения дисперсии при переходе в PLO из NLHE. Тщательный отбор столов для игры (хорошие столы в PLO найти достаточно легко) позволит сохранить ваш текущий винрейт в PLO, и свинги в Омахе окажутся не намного больше свингов в Холдеме. Особенно, если вы играете в солидном тайтово-агрессивном стиле, при котором дисперсия относительно невелика.

Теперь мы полностью готовы сформировать требования к величине банкролла. Мы рассчитали значения (или получили оценки) винрейта W, среднеквадратического отклонения S для нашей игры. Выбираем приемлемый низкий уровень риска разорения, например, 1% или 0.01. После чего подставляем эти три значения в формулу для расчета риска разорения и вычисляем величину стартового банкролла, при котором мы не превысим желаемый порог риска разорения.

Рассмотрим задачу расчета величины стартового банкролла на примере трех игр, с которыми мы имели дело в двух первых статьях этой серии.

3. Требования к величине банкролла для модельных игр

В качестве модельных игр в статьях данной серии мы рассматривали две игры в кубик (Игру в кубик 1 и Игру в кубик 2 с одинаковыми винрейтами, но разными дисперсиями) и AKQ-игру в покер. Мы вычислили значения винрейта и среднеквадратического отклонения для всех трех игр. Теперь мы собираемся вычислить необходимый размер стартового банкролла для трех уровней риска разорения – 10%, 5% и 1%.

3.1 Риск разорения для Игры в кубик 1

Игра с кубиком 1 имеет следующие условия:

• Ставка в игре  равна $1.
• При выпадении 1, 2, 3 и 4 ставка возвращается.
• При выпадении 5 мы проигрываем ставку.
• При выпадении 6 мы выигрываем две ставки.
• Математическое ожидание выигрыша EV = 0.1667.
• Дисперсия V = 0.8056.
• Среднеквадратическое отклонение SD = 0.8975.

Подставляем значения в формулу РР и получаем значения величины стартового банкролла для трех уровней толерантности к риску:

Округляем размер банкролла до ближайшего целого доллара и получаем:

• 10%  риска разорения соответствует банкроллу в $6
• 5%  риска разорения соответствует банкроллу в $7
• 1%  риска разорения соответствует банкроллу в $11

Другими словами, при низких требованиях к банкроллу отношение банкролла к величине ставки в игре равно 6. Хороший винрейт и низкая дисперсия (малое среднеквадратическое отклонение) позволяют начать игру с небольшим банкроллом.

Среди покерных игр пот-лимитная хай-лоу Омаха является хорошим примером игры с невысокими требованиями к размеру банкролла. Эта игра пока не очень популярна, для нее разработано мало хороших стратегий, так что в ней легко иметь очень хороший винрейт. Кроме того, правила игры способствуют низкой дисперсии. Например, вы можете часто фрироллить оппонентов и играть в больших банках, где вы или делите, или выигрываете целый банк. Это дает замечательное сочетание высокого винрейта и низкой дисперсии, что сводится к невысоким требованиям к величине стартового банкролла.

На рисунке представлен график размера банкролла как функции от риска разорения (от 1% до 50%) для Игры в кубик 1.

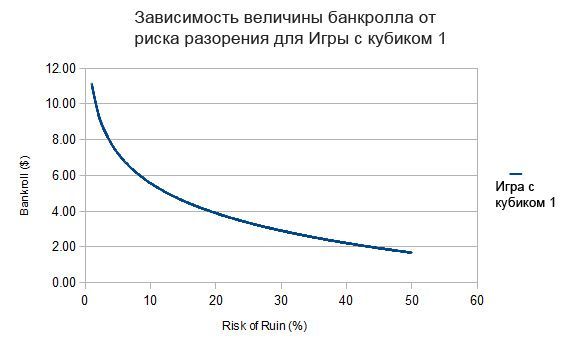
Размер требуемого банкролла монотонно уменьшается по мере роста нашей толерантности (при перемещении аргумента РР вправо)  к риску. Если мы стремимся к малому риску (левая часть области рисунка), требования к банкроллу резко возрастают. Если бы мы захотели на графике отразить область со значениями РР от 0% до 1%, мы бы увидели стремительный рост кривой по вертикальной оси вверх.

Перевод: Сергей 'ivolga' специально для pokeristby