Рациональный банкролл-менеджмент. Часть 3.2

Перевод данной статьи был осуществлен при поддержке покер рума William Hill Poker. William Hill Покер регулярно проводит эксклюзивные турниры для своих игроков, обеспечивает поддержку пользователей 24/7, гарантирует сохранность ваших средств, а также быстрые и удобные кешауты.

В данной статье мы закончим рассмотрение примеров игры с кубиками, которые начали в статье "Рациональный банкролл-менеджмент. Часть 3.1"

3.2 Риск разорения для Игры в кубик 2

Игра с кубиком 2 имеет следующие условия:

• Ставка в игре  равна $1.
• При выпадении 1, 2, 3, 4 и 5 мы проигрываем ставку.
• При выпадении 6 мы выигрываем шесть ставок.
• Математическое ожидание выигрыша EV = 0.1667.
• Дисперсия V = 6.8056.
• Среднеквадратическое отклонение SD = 2.6087.

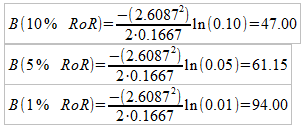
Округляем размер банкролла до ближайшего целого доллара и получаем:

• 10%  риска разорения соответствует банкроллу в $47 ($6 в Игре 1).
• 5%  риска разорения соответствует банкроллу в $61 ($7 в Игре 1).
• 1%  риска разорения соответствует банкроллу в $94 ($11 в Игре 1).

Другими словами, несмотря на одинаковые значения винрейта, для Игры с кубиком 1 требуется примерно в 8 раз больший банкролл по сравнению с Игрой в кубик 2.

Если мы можем выбирать из двух игр с одним и тем же винрейтом, но разными дисперсиями, нам следует выбрать игру с низкой дисперсией. В противном случае мы можем весь наш капитал потратить на одну эту игру вместо того, чтобы инвестировать его в другие игры и получать в них дополнительный доход. Игра с большей дисперсией повлечет за собой больший стресс и дискомфорт по причине даунсвингов большего размера.

С другой стороны, если вы обладаете хорошим самоконтролем, а у оппонентов он отсутствует, можно получить дополнительное преимущество в игре с большей дисперсией. Таким образом, не стоит бояться играть в игры с большими свингами, если ваш банкролл позволяет это, а на оппонентов дисперсия действует пагубно.

 PLO является одной из игр, где игроки с хорошим самоконтролем могут получить преимущество перед игроками с низким самоконтролем. В PLO много легче по сравнению с NLHE проиграть один или два стека и объяснить это сложной ситуацией, в которой можно было принять много различных правильных решений.

На рисунке представлены графики размера банкролла как функции от риска разорения (от 1% до 50%) для Игры в кубик 1 (синяя кривая) и Игры в кубик 2 (красная кривая).

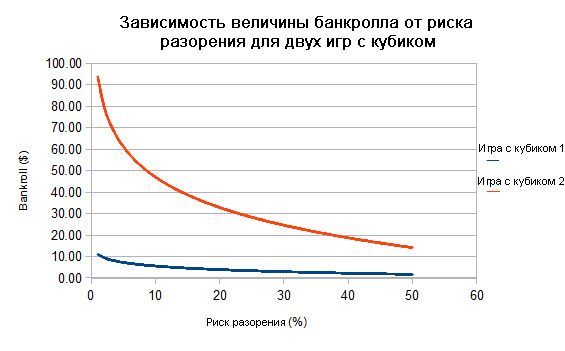
Из анализа графиков следует, что увеличение дисперсии в Игре с кубиком 2 приводит к необходимости играть с банкроллом, примерно в 8 раз превышающим банкролл для Игры с кубиком 1. Выше этот вывод был нами получен аналитически. Поскольку в обеих играх винрейт один и тот же, для нас в условиях свободы выбора нет смысла выбирать более дисперсионную игру.

Вместе с тем можно привести и доводы за игру в условиях большой дисперсии. Большие свинги создают иллюзию игры, в которой все основано на удаче. Это привлекает в игру слабых игроков. В малодисперсионной игре слабые игроки быстро убеждаются в своем слабом умении играть. А в играх с высокой дисперсией на своем пути к полной потере банкролла они могут попадать в большие апстрики и даунстрики. И они продолжают играть, поскольку начинают верить в свое мастерство (ведь однажды они выиграли так много, не правда ли?). В итоге это оказывает им плохую услугу.

Поскольку игры с высокой дисперсией привлекают слабых игроков, сильный игрок должен последовать за ними. Он может иметь примерно такой же винрейт в малодисперсионной игре, но такие игры могут оказаться  малораспространенными. Таким образом, чтобы наиграть много рук, необходимо играть в игры, в которых можно встретить множество слабых игроков.

Как уже было отмечено выше, можно иметь хороший винрейт в PLO8, которая относится к играм с малой дисперсией. Но в онлайне очень мало активных столов, на которых постоянно играют PLO8. Таким образом, трудно заработать себе на жизнь одним лишь гриндом на PLO8. Лучше в качестве своей основной дисциплины выбрать NLHE или PLO.

3.3 Риск разорения для AKQ-игры

Игра имеет следующие условия:

• В игру играют два игрока: Алиса (вне позиции) и Боб (в позиции).
• В начале игры оба игрока ставят анте в n bb. Это формирует начальный пот P = 2n bb.
• Оба игрока получают по одной случайной карты из AKQ-колоды.
• Алиса чекает "втемную".
• Теперь Боб может чекнуть и посмотреть шоудаун, а может и поставить 1 bb.
• Если Боб ставит 1 bb, Алиса может сфолдить, а может заколлировать ставку Боба и посмотреть шоудаун.
• После окончания раунда ставок, если никто из игроков не сфолдил, на шоудауне побеждает старшая карта.
• Математическое ожидание выигрыша EV = 5.56 bb/100.
• Среднеквадратическое отклонение SD = 10.79 bb/100.

Заметим, что в AKQ-игре винрейт выражен в bb/100 единицах, как это принято в покерных играх. Для нас выбор таких единиц не принципиален, поскольку мы используем их одновременно для винрейта и для среднеквадратического отклонения.

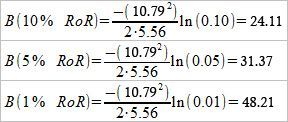
Округляем размер банкролла до ближайшего целого и получаем:

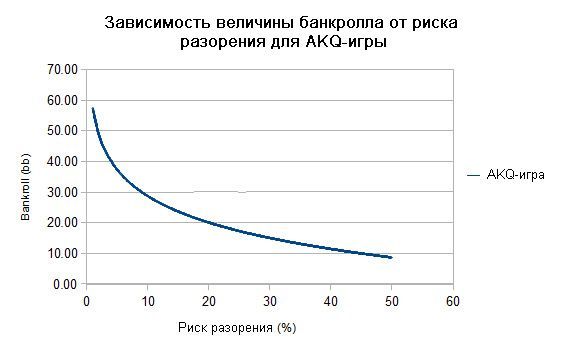
• 10% риска разорения соответствует банкроллу в 24 bb.
• 5% риска разорения соответствует банкроллу в 31 bb.
• 1% риска разорения соответствует банкроллу в 48 bb.

На рисунке представлен график размера банкролла как функции от риска разорения (от 1% до 50%)  для AKQ-игры.

4. Заключение

В данной статье мы добавили к средствам анализа схем банкролл-менеджмента еще одно понятие – риск разорения. Мы изучили формулу для расчета риска разорения, в которой соединены вместе винрейт, дисперсия / среднеквадратическое отклонение и размер стартового банкролла. В основном, мы используем формулу риска разорения в двух случаях:

• Для вычисления риска разорения (потери банкролла) при заданных значениях винрейта, среднеквадратического отклонения и размера банкролла.
• Для расчета величины банкролла, необходимого для игры при заданных значениях риска разорения, винрейта и среднеквадратического отклонения.

В трех первых статьях данной серии для анализа применимости математических методов мы использовали лишь простые модельные игры. В следующей статье мы перейдем к реальным покерным играм и рассчитаем величину необходимого банкролла для PLO и NLHE. Мы оценим типовые значения среднеквадратического отклонения для обеих игр и сформулируем требования, предъявляемые к размеру стартового банкролла в виде функции от винрейта. Также мы остановимся на других факторах (например, на стиле нашей игры), которые оказывают влияние на винрейт и среднеквадратическое отклонение.

Удачи! Багз.

Перевод: Сергей 'ivolga' специально для pokeristby